Coin Toss Game Examines Interplay of Skill and Fate

Americans tend to believe that abilities, traits, and efforts help anyone get ahead. This game examines the huge impact of social and economic factors.

EDITOR'S NOTE: Click here to play an online version of this game, with interactive options.

Americans tend to believe that opportunities to get ahead are available for everyone and that people's positions in the stratification order are a function of their abilities traits, and efforts, rather than social and economic factors. Given the beliefs that students bring with them to class, instructors must find creative ways to illustrate that structural factors can and do play a large role in the various stratification processes. We developed a classroom exercise for stratification and organization courses that demonstrates how social structures can constrain individual actions (Renzulli, Aldrich, and Reynolds, 2003).

This exercise uses the simple process of flipping coins to show students how individual actions, when aggregated at a system level, produce outcomes that look as if they could be the result of individual intentions, but are actually an outcome of structural constraints imposed on actions: the "rules of the game."

This exercise helps students understand that individual effort is not always the only factor in individual and organizational success. It is intended to show that forces other than (or in addition to) individual characteristics shape outcomes and distributions of societal rewards.

The Exercise

If students are accustomed to using individual explanations rather than reasoning with their sociological imaginations, structural rationales for stratification will be difficult for them to grasp. Instructors can assign readings that will set the stage for an instructional unit on stratification (who gets what and why?) or organizational sociology (the role of managerial talent versus chance).

Any reading that stresses structural forces as opposed to individual characteristics can be used as background reading for this exercise. We recommend the following:

• Davis and Moore's article "Some Principles of Stratification" (1944) is particularly useful for highlighting such oversights because it is a work that is both widely read and widely misunderstood by students in stratification classes.
• Black Wealth/White Wealth (Oliver and Shapiro 1977) is a particularly good reading for this exercise because Oliver and Shapiro very convincingly show that cumulative disadvantage and advantage processes generate the current distribution of wealth.
• Wealth Inequality in the United States (Keister & Moller, 2000)
• Getting Rich: America’s New Rich and How They Got That Way (Keister, 2005)
• Inequality by Design (Fischer et al. 1996)

This exercise could also be used with readings or materials that encourage students to think about the possible consequences of guaranteeing equality of opportunity or equality of outcomes. In particular, instructors may want to consider excerpts from:

• Michael Young's Rise of the Meritocracy (Young 1994)
• Kurt Vonnegut's short story (1968), "Harrison Bergeron," which was also made into a movie by the same name in 1995.

Advance Preparation

The game and the following discussion fill an entire class. The game fits best in a 75-minute class, but can be done in a 50-minute class; if instructors watch their time carefully.

In order to facilitate gameplay efficiently, the instructor can provide directions before class and put directions on a PowerPoint slide that remains up during class, demonstrate the flipping and betting process before the students start playing, and encourage students to bring five coins to class. Download the accompanying PowerPoint slides and use them for your class.

Setup and Rules

To set up the game, divide students into pairs and give each pair of students 10 coins (five per student). Then, give students time to understand how the game works.

It is important that the rules are written out and that students take time to review them carefully before the game begins. The basic game has only four rules:

1. One student in each pair bets on each flip (up to a maximum of three coins).
2. The winner of the bet takes the coins from the loser, regardless of who actually flipped the coin or made the bet.
3. Players must flip quickly and cannot stop betting.
4. Students cannot borrow money once they go bankrupt. When they run out of coins, they are out of the game.

At the start of the game, it is important to get students thinking about how the distribution of coins will change during the course of the game. To make the ultimate outcome as memorable as possible, instructors can start class with a simple question, "Who is so skilled at tossing a coin that they can guarantee that they will flip heads almost every time?"

Students often comment that they are skilled at flipping a coin into the air but cannot predict how it will land. Ask the students if they think the uniform distribution of coin flipping talent will lead to a random reshuffling of the coins and if it will preserve the uniform distribution of coins among the players; most students believe that it will. They reason that if no one is better at flipping than anyone else, then no one will get ahead.

Gameplay

The game consists of multiple rounds of coin tossing, with each round lasting about two minutes. During each round, students pair off, flip coins, and bet one to three coins on the outcome of each flip (heads or tails). The winner of each bet takes the specified number of coins from the loser. Winners then look for another person to play against for the remainder of the round. During the game, instructors should circulate through the room to identify students who are looking for others to play against and help them find new partners. When a student in a pair has lost all of their coins (i.e., gone bankrupt), they are out of the game and move to the back of the room and just observe.

After each two-minute round, instructors tally the number of people with 0, 1-4, 5-9, 10-15, and 16+ coins and post the results on the board, so that students can watch how quickly the distribution of coins becomes unequal. See figure 1 below.

Figure 1: Results of the Game

Whoever is still left with coins at the end of each round goes on to the next round and should begin to play with a new partner. The game ends when at least one person has 16+ coins, which can occur as early as the fifth round. By that point, many students are bankrupt. Most players finish with either no coins or 1-4 coins, and a small number of players has 10-15 or more. In a typical game with 50 students, three or four students will have 16 or more coins while 30 students will be left with no coins.

Discussion

Results of the game are highly predictable but also counter-intuitive to many students, and the success of the game depends on a good discussion afterward.

In order to discuss the importance of skill and talent, instructors can begin in a lighthearted way by asking the "winners" to account for their win. In most cases, they answer in one of three ways:

1. They sarcastically acclaim themselves as great achievers: "I used a well-thought-out strategy, and my skill led to success." This mocking comment indicates that students understand they could not have actually used a strategy.
2. They may be embarrassed to answer. Their embarrassment also shows that they feel foolish about taking credit for something they know they did not do.
3. Students may tell the class exactly what they did. For example, "I bet tails all the time." (And inevitably a "loser" in the class will proclaim that she did that too.)

To help illustrate the point that individual efforts do not make or break students’ success in the game, ask: “What would have happened if we played the game again? Who would be the winner?" Students realize that they could not predict who would win, and are certain that the winner of the original game would not win in subsequent games. They also realize that the distribution of the coins would ultimately be the same at the end of each game.

This simple set of questions quickly illustrates the difference between the probability of winning the game and the probability of flipping heads or tails. The probability of flipping heads or tails never changes: the chance of flipping heads is one in two every time. However, the probability of an individual surviving to the last round is much smaller and could, in fact, vary from person to person. In the end, the students begin to understand that their individual skill, action and intention did not make them winners or losers in this game.

Having established that skill and talent cannot explain the outcome, instructors can then point out that a very recognizable distribution still emerged. Results from the exercise can be displayed graphically by plotting the number of students on the vertical (Y) axis and the number of coins, from zero to n, on the horizontal (X) axis. Connect the dots to show a line dropping sharply from the upper left to the lower right. Some players became very wealthy, but most will become bankrupt, even though everyone started out with the same resources and played with the same skill and effort.

For comparison purposes in a class on inequality, instructors can bring to class a graph of the wealth distribution in the United States. In a class on organizations, bring a graph of the distribution of organizational size or corporate assets. The distributions are very similar and help students realize that inequality and personal success are not necessarily the result of personal attributes. (See figures 2 and 3.)

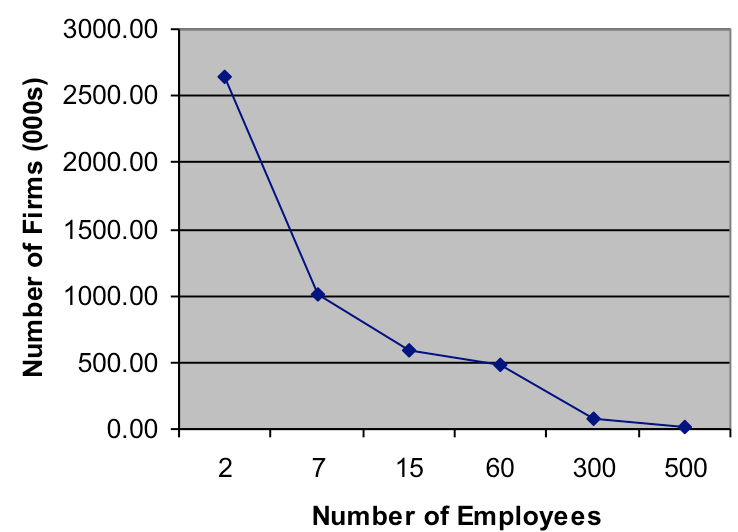
Figure 2: Distribution of Firm Size

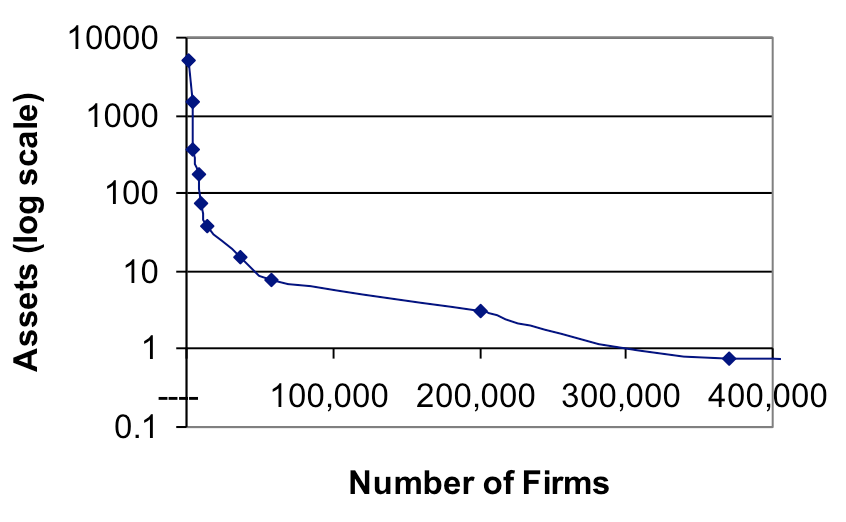
Figure 3:Distribution of Corporate Assets

To help students relate the game to real-world processes that generate inequality, instructors should discuss how modifications of the rules might alter the outcome:

1. What would happen if some players started the game with a different number of coins? We use this modification to talk about the importance of social origins. We point out that when a student with 10 coins bets three and loses, she has lost 30 percent of her assets but is still in a top bracket of winners with seven coins. By contrast, when students with three coins bet three and lose, they have lost 100 percent of their assets and are out of the game. In short, an initial advantage goes a long way toward success, whereas an initial disadvantage leaves students behind rather quickly (Oliver and Shapiro 1997). In life, the valued good may be education, or income, or wealth rather than coins, but initial advantages are still important.
2. What would happen if bankrupt players could borrow money to get back into the game? This is an opportunity to talk about the role of financial institutions, credit agencies, and other sources of capital. Large organizations, for instance, have access to huge amounts of credit and, in some cases, are not allowed to fail. In a similar fashion, some people have better access to credit than others and are thus better able to handle economic misfortune. In essence, the game provides a level playing field by denying everyone access to credit; but in the real world, people have unequal access to credit and thus different chances of amassing wealth or going broke.
3. What are the possible consequences of allowing some players to pool their resources and play as a group? In the game, everyone plays as an individual, but in real life, we are connected to groups of relatives, friends, and acquaintances who have economic and non-economic resources that can help or hinder our efforts to succeed.
4. What would happen if a wealth or inheritance tax had been imposed between rounds? This is an opportunity to talk about the inter-generational transfer of wealth in the United States (Keister & Moeller 2000), or income or property taxes and how taxes and the social welfare system might restrict the amount of income inequality in a society. The basic point is that societies usually limit inequality by imposing restrictions on the accumulation and transmission of wealth. The game provides no such safeguards.
5. What would happen if you could buffer yourself against losses? This brings up the options of withdrawing from the game or protecting against competition through local isolation or creation of IP, or other competitive barriers.

Ultimately, students should come to realize that the final distribution of coins and their personal chances of becoming a winner are not flukes, but rather the result of the rules of play that determine who gets the coins and why. They should also realize that even in the real world, where skill and effort do matter, their ability to get ahead and their chances of falling behind are also determined by taken-for-granted rules and structures of opportunities.

Conclusion

The coin toss provides a way to illustrate how sociological concepts can increase a student's understanding of the social world and supplement individual explanations. Playing the game encourages students to engage with the material and thus facilitates their understanding of it. Also, students find the game fun, as well as intellectually helpful.

Play it Online!

Play an interactive online version of the game here. 

References and Further Reading

Davis, Kingsley and Wilbert E Moore. 1944. “Some principles of stratification.” American Sociological Review, volume 10, number two, pages 244 – 249.

Fisher, Clyde S. Michael How, Martin Sanchez Jankowski, Samuel R Lucas, and Swidler, and Kim Voss. 1996. Inequality by Design: Cracking the Bell Curve Myth. Princeton University Press.

Keister, Lisa A. 2005. Getting Rich: America’s New Rich and How They Got That Way. Cambridge University press.

Keister, Lisa A and Stephanie Moeller. 2000. “Wealth inequality in the United States.” Annual Review of Sociology, Volume 26, pages 63 – 81.

Oliver, Melvin and Thomas M Schapiro, Editors. Black Wealth/White Wealth: a New Perspective on Racial Inequality, Second Edition. Routledge.

Linda Renzulli, Howard E. Aldrich, and Jeremy Reynolds. 2003. “It’s Up in the Air, or is It?” Teaching Sociology. 31, 1 (January): 49-59.

Vonnegut, Kurt. 1968. “Harrison Bergeron” in his collection of short stories, Welcome to the Monkey House. Delacorte press.

Young, Michael. 1994. The Rise of the Meritocracy. Transaction publishers. Originally published in 1958.

More ideas

College business professors looking for more ideas to enrich the classroom experience can find them here.

Additional Search Terms: entrepreneurship courses, teaching ideas, teaching resources, classroom ideas, entrepreneurship classes, business schools, business school classes, entrepreneurship students, professors